공부하자 동진아

스택

  - 데이터를 제한적으로 접근할 수 있는 구조

      • 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조

  - 가장 나중에 쌓은 데이터를 가장 먼저 빼낼 수 있는 데이터 구조

      • 큐 : FIFO 정책

      • 스택 : LIFO 정책

스택 구조

  - 스택은 LIFO(Last In, First Out) 또는 FILO(First In, Last Out) 데이터 관리 방식을 따름

      • LIFO : 마지막에 넣은 데이터를 가장 먼저 추출하는 데이터 관리 정책

      • FILO : 처음에 넣은 데이터를 가장 마지막에 추출하는 데이터 관리 정책

  - 대표적인 스택의 활용

      • 컴퓨터 내부의 프로세스 구조의 함수 동작 방식

  - 주요 기능

      • push() : 데이터를 스택에 넣기

      • pop() : 데이터를 스택에서 꺼내기

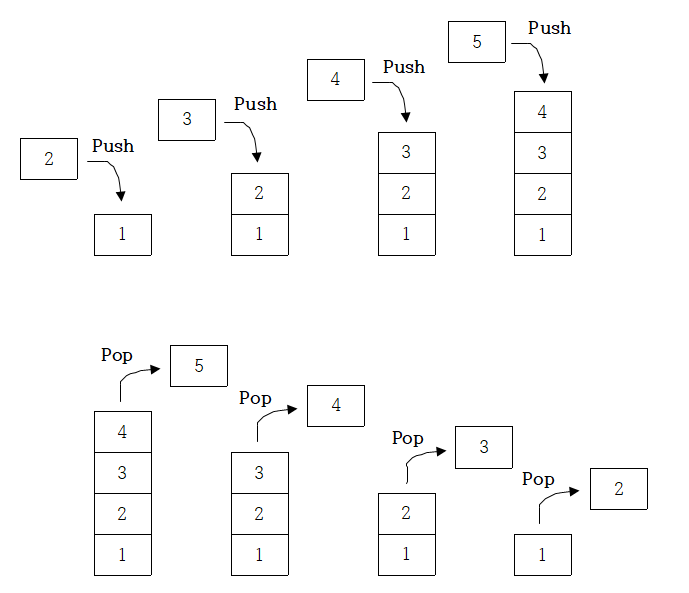
스택 구조와 프로세스 스택

  - 장점

      • 구조가 단순해서, 구현이 쉽다.

      • 데이터 저장/읽기 속도가 빠르다.

  - 단점

      • 데이터 최대 개수를 미리 정해야 한다.

      • 저장 공간의 낭비가 발생할 수 있음

파이썬 리스트 기능에서 제공하는 메서드로 스택 사용해보기

  - append(push), pop 메서드 제공

data_stack = list()

data_stack.append(1)
data_stack.append(2)

print(data_stack)		# [1, 2]
print(data_stack.pop())	# 2

  - pop(), push() 기능 구현해보기

stack_list = list()

def push(data):
	stack_list.append(data)

def pop():
	data = stack_list[-1]
	del stack_list[-1]
	return data

for index in range(10):
	push(index)

print(pop())	# 9

큐 구조

  - 줄은 서는 행위와 유사

  - 가장 먼저 넣은 데이터를 가장 먼저 꺼낼 수 있는 구조, '선입선출' 구조의 자료구조

  - FIFO(First In, First Out) 방식으로 스택과 꺼내는 순서가 반대

알아둘 용어

  - Enqueue : 큐에서 데이터를 넣는 기능

  - Dequeue : 큐에서 데이터를 꺼내는 기능

파이썬 queue 라이브러리 활용해서 큐 자료 구조 사용하기

  - queue 라이브러리에는 다양한 큐 구조로 Queue(), LifoQueue(), PriorityQueue() 제공

      • Queue() : 가장 일반적인 큐 자료 구조

      • LifoQueue() : 나중에 입력된 데이터가 먼저 출력되는 구조 (스택구조)

      • PriorityQueue() : 데이터마다 우선순위를 넣어서, 우선순위가 높은 순으로 데이터 출력

        PriorityQueue((우선순위, 데이터))

참고 : 어디에 큐가 많이 쓰일까?

  - 멀티 태스킹을 위한 프로세스 스케쥴링 방식을 구현하기 위해 많이 사용됨 (운영체제 참조)

파이썬을 활용한 Queue(), LifoQueue(), PriorityQueue() 구현

  - Queue()

import queue

data_queue = queue.Queue	# queue 라이브러리에 있는 Queue 사용

data_queue.put('dongjin')
data_queue.put(1)

print(data.queue.qsize())	# 2
print(data.queue.get())		# 'dongjin'
print(data.queue.qsize())	# 1

  - LifoQueue()

import queue

data_queue = queue.LifoQueue	# queue 라이브러리에 있는 LifoQueue 사용

data_queue.put('dongjin')
data_queue.put(1)

print(data.queue.qsize())	# 2
print(data.queue.get())		# 1

  - PriorityQueue()

import queue

data_queue = queue.PriorityQueue	# queue 라이브러리에 있는 PriorityQueue 사용

data_queue.put((10, 'dongjin'))
data_queue.put((5, 1))
data_queue.put((12, 'korea'))

print(data.queue.qsize())	# 3
print(data.queue.get())		# (5, 1)
print(data.queue.get())		# (10, 'dongjin')

리스트 변수로 큐를 다루는 enqueue, dequeue 기능 구현

queue_list = list()

def enqueue(data):
	queue_list.append(data)
    
def dequeue():
	data = queue_lsit[0]
	del queue_list[0]
	return data
    
for index in range(10):
	enqueue(index)
    
print(len(queue_lsit))		# 10
print(dequeue())		# 0

정의

  - 동적 계획법 (DP 라고 많이 부름)

      • 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결,

            최종적으로 전체 문제를 해결하는 알고리즘

      • 상향식 접근법으로, 가장 최하위 답을 구한 후 저장, 해당 결과 값을 이용해서 상위 문제를 풀어가는 방식

      • Memoization 기법을 사용

          • Memoization (메모이제이션) 이란?

              • 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 실행 속도를 빠르게 하는 기술

      • 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨

          • 예 : 피보나치 수열

  - 분할 정복

      • 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘

      • 하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식

          • 일반적으로 재귀함수로 구현

      • 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음

          • 예 : 병합 정렬, 퀵 정렬 등

공통점과 차이점

  - 공통점

      • 문제를 잘게 쪼개서, 가장 작은 단위로 분할

  - 차이점

      • 동적 계획법

          • 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨

          • Memoization 기법 사용(부분 문제의 답을 저장해서 재활용하는 최적화 기법으로 사용)

      • 분할 정복

          • 부분 문제로 서로 중복되지 않음

          • Memoization 기법 사용 안함

동적 계획법 알고리즘 이해 (피보나치 수열)

  - recursive call 활용

def fibonacci(num):
	if num <= 1:
		return num
	return fibonacci(num + 1) + fibonacci(num + 2)

print(fibonacci(10))		# 55

  - 동적 계획법 활용

def fibonacci_dp(num):
	cache = [index for index in range(num + 1)]		# list comprehension
	cache[0] = 0
	cache[1] = 1

	for index in range(2, num + 1):
		cache[index] = cache[index - 1] + cache[index - 2]
	return cache[num]

print(fibonacci_dp(10))		# 55

재귀 용법(recursive call, 재귀 호출)

  - 함수 안에서 동일한 함수를 호출하는 형태

  - 여러 알고리즘 작성 시 사용되므로, 익숙해져야 한다.

예제

  - 팩토리얼 구하는 알고리즘 작성하기

  - 2! = 1 * 2

     3! = 1 * 2 * 3

     4! = 1 * 2 * 3 * 4

     규칙 : n! = n * (n-1)!

def factorial(num):
	if num > 1:
		return num * factorial(num - 1)
	else:
		return num	# 재귀 함수 종료
        
print(factorial(10))	# 362880

  - factorial() 함수를 호출할 때마다, 지역변수 n 이 생성됨

  - 시간 복잡도 / 공간 복잡도는 O(n)

  - 함수는 내부적으로 스택처럼 관리된다.

  - 리스트 총 합 알고리즘 작성하기

def sum_list(data):
	print(data)
	if len(data) == 1:
		return data[0]
	return data[0] + sum_list(data[1:])

data_list = [1, 2, 3, 4, 5]

print(sum_list(data_list))

#  [1, 2, 3, 4, 5]
#  [2, 3, 4, 5]
#  [3, 4, 5]
#  [4, 5]
#  [5]
#  15