공부하자 동진아

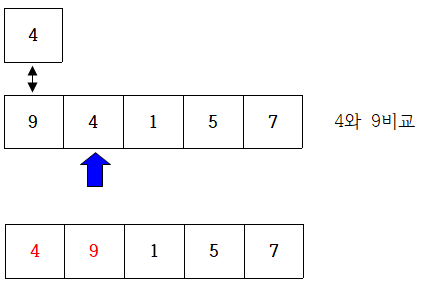
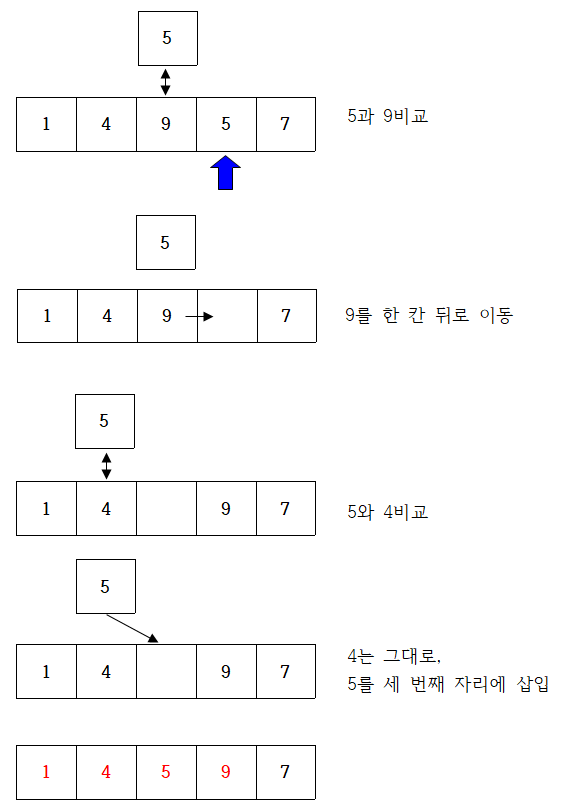
선택 정렬이란?

  - 다음과 같은 순서를 반복하며 정렬하는 알고리즘

      1. 주어진 데이터 중, 최솟값을 찾음

      2. 해당 최솟값을 데이터 맨 앞에 위치한 값과 교체

      3. 맨 앞의 위치를 뺀 나머지 데이터를 동일한 방법으로 반복

단계별로 생각하기

  - 예 : data_list = [5, 19, 3, 14]

  - 1차 로직

4개의 값 중에서 가장 작은 값 3을 제일 앞에 있는 5와 교체

맨 앞에 위치한 3고정

  - 2차 로직

맨 앞의 위치를 뺀 나머지 값에서 가장 작은 값 5를 19와 교체

앞으로 위치한 5고정

  - 3차 로직

고정 값을 제외한 나머지 값에서 가장 작은 값 14와 19교체

정렬 완료

알고리즘 구현

def selection_sort(data):
	for stand in range(len(data) - 1):
		lowest = stand
		for index in range(stand + 1, len(data)):
			if data[lowest] > data[index]:
				lowest = index
		data[lowest], data[stand] = data[stand], data[lowest]
	return data
    
data_list = [5, 19, 3, 14]
print(selection_sort(data_list))	# [3, 5, 14, 19]

정리

  - 버블 정렬과 성능상 큰 차이가 없다.

  - 비교연산에 대한 빅-오는 최악의 경우와 최선의 경우 구분 없이 O(n^2)이다.

  - 이동연산에 대한 빅-오는 최악의 경우와 최선의 경우 구분 없이 O(n)이다.

삽입 정렬이란?

  - 삽입 정렬은 두 번째 인덱스부터 시작하여 그 앞의 데이터들과 비교하여 삽입할 위치를 지정한 후

     데이터를 뒤로 옮기고 지정한 자리에 삽입하여 정렬하는 알고리즘

단계별로 생각하기

  - 예 : data_list = [9, 4, 1, 5, 7]

  - 두 번째 인덱스부터 시작

  - 앞의 데이터들과 비교하여 삽입할 위치를 지정 후, 데이터를 뒤로 옮기고 지정한 자리에 삽입

  - n개의 리스트가 있는 경우 최대 n-1번의 로직 적용

  - 1차 로직

  - 2차 로직

  - 3차 로직

  - 4차 로직

알고리즘 구현

def insertion_sort(data):
	for index in range(len(data) - 1):	# 로직 횟수
		for index2 in range(index + 1, 0, -1):	# index+1에서부터 -1씩 빼면서 1까지, range[start, stop, step]
			if data[index2] < data[index2 - 1]:
				data[index2], data[index2 - 1] = data[index2 - 1], data[index2]
			else:
				break
	return data
    
data_list = [9, 4, 1, 5, 7]
print(insertion_sort(data_list))	# [1, 4, 5, 7, 9]

정리

  - 비교연산과 이동연산에 대한 빅-오는 O(n^2)이다.

  - 보는 관점에 따라서 별도의 메모리를 필요로 하지 않는 '개선된 선택 정렬'과 유사하다고 느낄 수 있다.

버블 정렬이란?

   - 두 인접한 데이터를 비교해서, 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘

단계별로 생각하기

   - 예 : data_list = [9, 4, 1, 5]

   - n개의 리스트가 있는 경우 최대 n-1번의 로직 적용

   - 로직을 1번 적용할 때마다 큰 숫자가 뒤에서 1개씩 결정

   - 데이터 교환이 없으면 로직을 반복 적용할 필요 없음

   - 1차 로직

   - 2차 로직

   - 3차로직

알고리즘 구현

def bubble_sort(data):
	for index in range(len(data) - 1):	# 로직 횟수
		swap == False
		for index2 in range(len(data) - index - 1):	# 로직 1회 할 때마다 뒤에 수가 결정되므로
			if data[index2] > data[index2 + 1]:
				data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
				swap == True
		if swap == False:
			break
	return data         
             
data_list = [9, 4, 1, 5]
print(bubble_sort(data_list))	# [1, 4, 5, 9]

정리

   - 비교연산에 대한 빅-오는 최악의 경우와 최선의 경우 구분 없이 O(n^2)이다.